微积分的发展史|微积分的发展

微积分的发展史|微积分的发展

微积分是微分和积分两门学问的统称，研究的范畴有三，包括微分、积分，以及微分和积分两者之间的关系。微分主要讨论一个变量怎样随时间（或其他变量）改变，而积分则主要讨论计算面积的方法。它们两者的关系由「微积分基本定理」（或称「牛顿－莱布尼茨公式」）给出：简单来说，这条定理说明，在适当的条件下，求积分是求微分之逆，求微分也是求积分之逆。以下简介微积分发展的歷史。
　　
　　一、萌芽时期
　　
　　早在希腊时期，人类已经开始讨论「无穷」、「极限」以及「无穷分割」等概念。这些都是微积分的中心思想；虽然这些讨论从现代的观点看有很多漏洞，有时现代人甚至觉得这些讨论的论証和结论都很荒谬，但无可否认，这些讨论是人类发展微积分的第一步。
　　
　　例如公元前五世纪，希腊的德謨克利特（Democritus）提出原子论：他认為宇宙万物是由极细的原子构成。在中国，《庄子．天下篇》中所言的「一尺之捶，日取其半，万世不竭」，亦指零是无穷小量。这些都是最早期人类对无穷、极限等概念的原始的描述。
　　
　　其他关於无穷、极限的论述，还包括芝诺（Zeno）几个著名的悖论1：其中一个悖论说一个人永远都追不上一隻乌龟2，因為当那人追到乌龟的出发点时，乌龟已经向前爬行了一小段路，当他再追完这一小段，乌龟又已经再向前爬行了一小段路。芝诺说这样一追一赶的永远重覆下去，任何人都总追不上一隻最慢的乌龟－－当然，从现代的观点看，芝诺说的实在荒谬不过；他混淆了「无限」和「无限可分」的概念。人追乌龟经过的那段路纵然无限可分，其长度却是有限的；所以人仍然可以以有限的时间，走完这一段路。然而这些荒谬的论述，开啟了人类对无穷、极限等概念的探讨，对后世发展微积分有深远的歷史意味。
　　
　　另外值得一提的是，希腊时代的阿基米德（Archimedes）已经懂得用无穷分割的方法正确地计算一些面积，这跟现代积分的观念已经很相似。由此可见，在歷史上，积分观念的形成比微分还要早－－这跟课程上往往先讨论微分再讨论积分刚刚相反。
　　
　　二、十七世纪的大发展－－牛顿和莱布尼茨的贡献
　　
　　中世纪时期，欧洲科学发展停滞不前，人类对无穷、极限和积分等观念的想法都没有甚麼突破。中世纪以后，欧洲数学和科学急速发展，微积分的观念也於此时趋於成熟。在积分方面，一六一五年，开普勒（Kepler）把酒桶看作一个由无数圆薄片积累而成的物件，从而求出其体积。而伽利略（Galileo）的学生卡瓦列里（Cavalieri）即认為一条线由无穷多个点构成；一个面由无穷多条线构成；一个立体由无穷多个面构成。这些想法都是积分法的前驱。
　　
　　在微分方面，十七世纪人类也有很大的突破。费马（Fermat）在一封给罗贝瓦（Roberval）的信中，提及计算函数的极大值和极小值的步骤，而这实际上已相当於现代微分学中所用，设函数导数為零，然后求出函数极点的方法。另外，巴罗（Barrow）亦已经懂得透过「微分三角形」（相当於以dx、dy、ds為边的三角形）求出切线的方程，这和现今微分学中用导数求切线的方法是一样的。由此可见，人类在十七世纪已经掌握了微分的要领。
　　
　　然而，直至十七世纪中叶，人类仍然认為微分和积分是两个独立的观念。就在这个时候，牛顿和莱布尼茨将微分及积分两个貌似不相关的问题，透过「微积分基本定理」或「牛顿－莱布尼茨公式」连繫起来，说明求积分基本上是求微分之逆，求微分也是求积分之逆。这是微积分理论中的基石，是微积分发展一个重要的里程碑。
　　
　　微积分诞生以后，逐渐发挥出它非凡的威力，过去很多初等数学束手无策的问题，至此往往迎刃而解。例如，雅各布．伯努利（JakobBernoulli）用微积分的技巧，发现对数螺线经过各种适当的变换之后，仍然是对数螺线3。他的弟弟约翰．伯努利（JohnannBernoulli）在一六九六年提出一个「最速降线」问题︰「一质点受地心吸力的作用，自较高点下滑至较低点，不计摩擦，问沿著什麼曲线，时间最短？」这条问题后来促使了变分学诞生4。欧拉（Euler）的《引论》、《微分学》、《积分学》亦总结了自十七世纪微积分的全部成果。
　　
　　儘管如此，微积分的理论基础问题，仍然在当时的数学界引起很多争论5。牛顿的「无穷小量」，有时是零，有时又不是零，他的极限理论也是十分模糊的。莱布尼茨的微积分同样不能自圆其说。这个问题要到十九世纪才得到完满的解答，所以微积分在当时，惹来不少反对的声音，当中包括数学家罗尔（Rolle）。儘管如此，罗尔本身亦曾提出一条与微积分有关的定理︰他指出任意的多项式f(x)=a+bx+cx2+dx3+...的任何两个实根之间都存在至少一个b+2cx+3dx2+...的实根。熟悉微积分的朋友会知道，b+2cx+3dx2+...其实是f(x)=a+bx+cx2+dx3+...的导数6。后人将这条定理推广至可微函数，发现若函数f(x)可微，则在f(x)=0的任何两个实根之间，方程f"(x)=0至少有一个实根。这条定理被冠為「罗尔定理」，是為微分学的基本定理之一。由此可见，在挑战微积分的理论基础的同时，数学家已经就微积分的发展作出了很大的贡献。
　　
　　三、十九世纪基础的奠定
　　
　　微积分的发展迅速，使人来不及检查和巩固微积分的理论基础。十九世纪，许多迫切问题基本上经已解决，数学家於是转向微积分理论的基础重建，人类亦终於首次给出极限、微分和积分等概念的严格定义。
　　
　　一八一六年，波尔查诺（Bolzano）在人类歷史上首次给出连续函数的近代定义。继而在一八二一年，柯西（Cauchy）在他的《教程》中提出e方法，后来在一八二三年的《概要》中他改写為d方法，把整个极限过程用不等式来刻画，使无穷的运算化為一系列不等式的推算，这就是所谓极限概念的「算术化」。后来外尔斯特拉斯（Weierstrass）将e和d联繫起来，完成了e-d方法，这就是现代极限的严格定义。
　　
　　有了极限的严格定义，数学家便开始尝试严格定义导数和积分。在柯西之前，数学家通常以微分為微积分的基本概念，并把导数视作微分的商。然而微分的概念模糊，把导数定义作微分的商因此并不严谨。於是柯西《概要》中直接定义导数為差商的极限，这就是现代导数的严格定义，是為现代微分学的基础。
　　
　　在《概要》中，柯西还给出连续函数的积分的定义：设f(x)為在[a,b]上连续的函数，则任意用分点a=x0<...<xn=b，将[a,b]分為n个子区间[xi-1,xi](i=1,2,...,n)，若果和式
　　
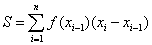
　　当最大子区间的长度趋向0时，极限存在，则此极限称為函数f(x)在[a,b]上的积分。这跟现代连续函数积分的定义是一致的。
　　
　　后来黎曼（Riemann）推广了柯西的定义。黎曼的定义跟柯西的定义不同的地方，在於和式S的定义：在黎曼的定义中，和式S定义為
　　
　　（留意黎曼在黎曼和中用了[xi-1,xi]中任意一点xi-1，而柯西在其和式S中则永远选取子区间[xi-1,xi]的左端点xi-1）。我们说黎曼推广了柯西的定义，是因為对所有在[a,b]上连续的函数，柯西积分的值跟黎曼积分的值一样，而且有一些在[a,b]上不连续的函数，当最大子区间的长度趋向0时S的极限依然存在。这就是现在所用的「黎曼积分」的定义；至此微积分理论的基础重建已经大致完成。
　　
　　柯西以后，微积分逻辑基础发展史上的最重大事件是人类从集合理论出发，建立了实数理论－－我们说实数理论的建立是微积分理论发展史上的一件大事，是因為微积分的理论用上了很多实数的性质。这实数理论的建立，主要功劳归於戴德金（Dedekind）、康托尔（Cantor）、外尔斯特拉斯等人。一八七二年，梅雷（Méray）提出的无理数定义，和同一年康托尔提出用有理「基本序列」来定义无理数实质相同。有了实数理论，加上集合论和极限理论，微积分就自从三百年以来，首次有了巩固的逻辑基础，而微积分的理论亦终於趋於完备。
　　
　　註：
　　
　　1.悖论是一些似是而非的推论；这些推论在逻辑上都是不成立的。当然，在这个例子里，我们现在知道芝诺提出的是悖论，是因為我们现在有一套已经发展得很完备的逻辑系统。在芝诺的时代，芝诺以至其他学者都还没有意识到其推论的谬误。[返回原文]
　　
　　2.歷史上那个追乌龟的人名叫阿基琉斯（Achilles）。[返回原文]
　　
　　3.在惊叹和欣赏这曲线的神奇巧妙之餘，他要求死后将对数螺线刻在自己的墓碑上，并附以颂词「纵使变化，依然故我！」。[返回原文]
　　
　　4.变分学是微积分的一个分支。[返回原文]
　　
　　5.另外，牛顿比莱布尼茨早十年研究微积分，但莱布尼茨却比牛顿早三年发表研究结果，这引发了微积分发明优先权的争论。[返回原文]
　　
　　6.不熟悉微积分的朋友，可把b+2cx+3dx2+...看作用0、1、2、……各项分别乘原多项式f(x)=a+bx+cx2+dx3+...各项再除以x所得到的方程。（来源：数学资料库）

微积分的发展史|微积分的发展

https://m.oubohk.cn/shuxue/153417/